Dies ist eine alte Version des Dokuments!
Halstead Category Test
Abkürzungen: HCT, CT
Hintergrund
Der Category Test wurde in den 30er und 40er Jahren des letzten Jahrhunderts von Ward Halstead entwickelt1). Er prüft die Fähigkeit zur abstrakten Konzeptbildung. Die zu lösende Aufgabe besteht darin, ein Ordnungskonzept zu finden, nach dem vier einfachen geometrischen Mustern, die nebeneinander dargestellt sind, eine Zahl zwischen eins und vier zugeordnet werden kann. Das Konzept muss frei gefunden werden. Wäre das Beispiel-Item in Abbildung 1 das erste in einem Subtest (die Subtests folgen jeweils dem gleichen Konzept), dann könnte man darauf mit der Zahl 2 antworten, weil das zweite Quadrat abweichend von allen anderen blau ist. Die Zahl 2 könnte aber auch deshalb richtig sein, weil das Konzept durch die Anzahl der großen Quadrate gegeben ist. Natürlich wäre auch denkbar, dass es - ganz im Gegenteil - die Anzahl der kleinen Quadrate ist. Man muss also zunächst raten. Aber selbst wenn die Antwort (hier die Antwort „2“) bei diesem Bild richtig ist, klärt sich erst durch die Anwendung des erdachten Konzepts auf nachfolgende Bilder, ob das dahinter vermutete Konzept tatsächlich das Richtige ist.
In Halsteads Originalversion wurden die Bilder dem Probanden von einem Apparat präsentiert. Der Proband drückte als Antwort einen von vier Knöpfen, was entweder mit einem Glockenklang (bedeutete richtig) oder einem Schnarren (bedeutete falsch) quittiert wurde. Eine Interaktion mit dem Versuchsleiter, der den Apparat damals noch von Hand steuerte, sollte nicht erfolgen. Halsteads Originalversion wurde anfangs der 50er Jahre von Reitan2) überarbeitet und bildete in dieser Fassung einen der wichtigsten Subtests der Halstead-Reitan Neuropsychological Test Battery. Bis in die 90er Jahre dürften die meisten HCT-Tests mit dieser Version durchgeführt worden sein.
Abbildung 1: Beispiel-Item des HCT
Als preiswertere Alternative zu dem unhandlichen Originalgerät entstanden in den 70er und 80er Jahren Papier-Bleistift-Versionen des HCT, von denen sich diejenige von DeFillippis und McCampbell (1991)3) international am meisten durchgesetzt hat. Ein Problem der Papier-Bleistift-Versionen ist es, dass die Interaktion mit dem Testleiter notwendigerweise intensiver ist als bei den Apparate- oder Computerversionen. Über die Jahre wurden auch eine Reihe von Kurzformen publiziert, von denen sich keine durchgesetzt hat.
Von Fast und Engel4) wurde 2007 eine Computerfassung für das „Hogrefe Test System 4“ publiziert. Sie ist inzwischen vergriffen. Von der Durchführungssituation her war diese Version der Originalversion ähnlich. Im zugehörigen Handbuch wurde ausführlich auf das Konzept und den Hintergrund des HCT eingegangen. Eine andere Computerversion wird vom „Neuropsychology Center (NPC)“ angeboten. Das NPC ist eine Firma in Texas, die seit einiger Zeit alle Verfahren der klassischen Halstead-Reitan Neuropsychological Battery neu aufgelegt hat und weltweit vertreibt.
Halsteads Category Test wird auch in allen wichtigeren englischsprachigen Lehrbüchern der neuropsychologischen Diagnostik besprochen 5) 6) 7).
Testmaterial
In der ersten Testversion bestand der Category Test aus neun Subtests mit 336 Items 8). Die heute übliche, von Ralph Reitan zu Beginn der 50er Jahre überarbeitete Fassung hat sieben Subtests mit 208 Items 9). Fast alle häufiger angewendeten Versionen des HCT bestehen aus diesen 208 Items, auch die deutsche Fassung des Tests von Fast und Engel 10).
Copyright
Die Copyright-Situation ist etwas unübersichtlich. Es gibt immer noch eine Webseite des „Reitan Neuropsychology Laboratory“, auch wenn sie 2012 für einige Zeit verwaist zu sein schien. Dort wird unter anderem darauf hingewiesen, dass es wichtig ist, mit den Originalmaterialien zu arbeiten, mit denen auch die meisten Normierungsuntersuchungen entstanden sind. Allerdings wurde nicht explizit ein Copyright für die Materialien reklamiert. Vermutlich wäre es auch ausgelaufen, weil die Originalbilder in den 30er Jahren entstanden sind. Andere Versionen des HCT, zum Beispiel die bei PAR in Florida erschienene Booklet-Version, sind ihrerseits Copyright-geschützt. Für die deutsche Version im Hogrefe Test-System 4 wurden die HCT-Bilder nach den alten Original-Vorlagen neu erstellt. Für diese Realisation des Verfahrens liegt das Copyright beim Verlag Hogrefe.
Testdurchführung
Die meisten Untersuchungen in der Literatur sind vermutlich mit einem der „HCT-Apparate“ aus Reitans Neuropsychological Laboratory durchgeführt worden, zumindest die älteren. Die deutsche Computerversion von Fast und Engel 11) kommt dieser Version sehr nahe. Das Gemeinsame daran ist die mechanische Form der Rückmeldung an den Probanden, bei der ein angenehmer Ton „richtig“ und ein unangenehmes Geräusch „falsch“ signalisiert.
Bei den Papier-Bleistift-Varianten muss der Versuchsleiter diese Aufgabe übernehmen. In der Praxis ist dies nicht so einfach: Gerade Patienten, die nicht so fit sind, fragen natürlich bei einer „falsch“-Antwort immer nach und wollen wissen, was an der Antwort denn falsch sei. Auf solche Fragen darf der Testleiter keine Antwort geben. Er darf nur die allgemeine Instruktion wiederholen („… Sie sollen herausfinden, welche Zahl dieses Bild darstellt…“). Bei einer verbalen Rückmeldung durch den Versuchsleiter erzeugt dieses eingeschränkte Antwortverhalten in der Praxis mehr Reaktanz auf Seiten der Patienten als wenn dies eine Maschine macht.
Ansonsten ist die Durchführung gleich: alle Items von 1 bis 208 werden präsentiert. Die Items sind in 7 Subtests aufgegliedert, von denen jeder noch einmal eine eigene Subtestinstruktion hat.
Testrohwerte
Apparat, Computer oder Testleiter notieren bei jedem Item die Antwort. Es gibt nur einen Testrohwert, nämlich die Anzahl der Fehler über alle 208 Items.
Verteilungseigenschaften der Rohwerte
Junge gesunde Erwachsene machen im HCT durchschnittlich zwischen 20 und 30 Fehler. Theoretisch könnte die Fehlerzahl bei 208 Items zwischen 0 und 208 schwanken, praktisch ist die Streubreite eingeschränkter. Der untere Rand der Fehlerverteilung ergibt sich daraus, dass man kaum weniger als 8 Fehler machen kann. Bei den ersten Items einer Serie muss man nämlich raten, weil man das Konzept nicht a priori kennen kann. Am oberen Rand der Fehlerverteilung gibt die Ratewahrscheinlichkeit eine gewisse Grenze vor. Rät ein Proband durchgehend, könnte man (als Mittelwert über mehrere solcher Rateübungen) 52 Richtige (208/4) und demnach 156 Fehler (208-52) erwarten. Auch wenn so ein Ergebnis in der Praxis extrem selten ist, kommen Fehlerzahlen von rund 100 durchaus vor, vor allem auch bei alten Probanden.
Bei der leistungsstarken Hälfte der Probanden liegen die Fehler also in einem sehr engen Schwankungsbereich, sagen wir zwischen 8 und 25. Bei der leistungsschwächeren Hälfte ist die Variabilität dagegen viel größer, sie schwankt zwischen 25 und 100. Solche Randbedingungen müssen zu einer linksgipfligen Verteilung der Rohwerte führen.
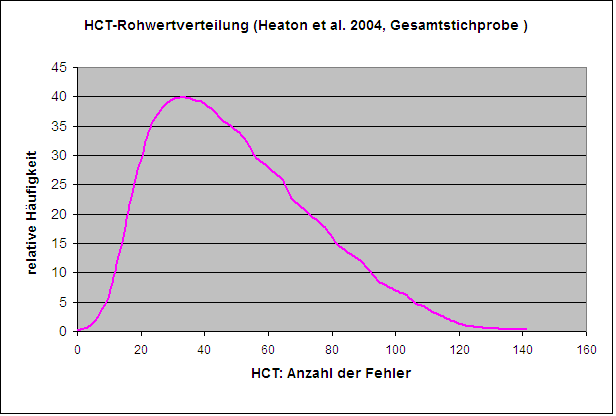
Empirische Daten dazu stehen in der Normensammlung von Heaton et al. (2004)12) zur Verfügung. Dort sind die Ergebnisse von 634 weißen und 578 schwarzen Amerikanern im Altersbereich zwischen 20 und 85 Jahren in einer Reihe von Tests, darunter der HCT, zusammengestellt. Die Autoren wandelten die Rohwerte über eine Flächentransformation (über alle Personen der Stichprobe hinweg) in Wertpunkte (Mittelwert 10, Standardabweichung 3) um und stellten das Ergebnis als Wertetabelle (Rohwert zu Wertpunkt) dar. Daraus ließen sich (nach Verstetigung und Glättung der groben Wertpunktskala) die Originalverteilungen der Daten auf der Ebene der Fehler zurückrechnen. Abbildung 2 zeigt die so rückgerechnete Rohwertverteilung über die 1212 Personen starke Gesamtstichprobe.
Abbildung 2: Häufigkeitsverteilung der HCT-Rohwerte in der Gesamtstichprobe (N=1212) von Heaton et al. (2004)
Wie zu erwarten, ist die Rohwertverteilung ziemlich linksgipflig und damit ohne nicht-lineare Transformation nicht gut interpretierbar. Zwei Beispiele sollen das illustrieren:
- Eine direkte Folge von schiefen Verteilungen ist die unangenehme Eigenschaft, dass gleich große Differenzen an verschiedenen Stellen der Skala Unterschiedliches bedeuten. Der Unterschied zwischen 15 und 20 Fehlern ist inhaltlich gravierender als der zwischen 75 und 80 Fehlern. Die Rohwertskala spiegelt das aber nicht wieder.
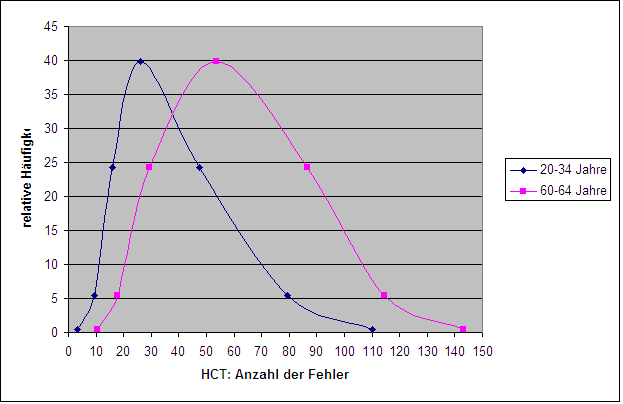
- Schiefe Verteilungen haben eine weitere unangenehme Eigenschaft. Bei beliebigen leistungsunterschiedlichen Subgruppen, also zum Beispiel bei Alterskohorten, sind die Standardabweichungen nicht gleich, sondern sie korrelieren positiv mit den Mittelwerten. An Hand der Daten von Heaton et al. (2004) lässt sich auch das gut zeigen. In Abbildung 3 sind die aus den Perzentiltabellen rückgerechneten Rohwertverteilungen von weißen Frauen und Männern mit 12-jähriger Schulbildung in zwei Altersgruppen im HCT gegenübergestellt, blau die Altersgruppe 20 bis 34 Jahre, rot die 60-64-Jährigen. Es lässt sich auf einen Blick erkennen, dass die Verteilung bei den älteren Probanden breiter ist als bei den Jüngeren, entsprechend dem höheren Mittelwert. Diese Verbreiterung geht aber zum größten Teil nicht auf eine größere Variabilität des Merkmals selbst zurück, sondern auf die Eigenschaften der Fehlerskala, die das psychologische Merkmal verzerrt abbildet, weil sie nach einer Seite ein festes Limit hat (Null Fehler) und nach der anderen Seite weiträumig offen ist (Limit 208 Fehler), der Mittelwert aber ziemlich nahe an einer der Seiten liegt. Dies macht sich bei den Jüngeren, im Durchschnitt Leistungsstärkeren, mehr bemerkbar als bei den Älteren.
Abbildung 3: Rückgerechnete Häufigkeitsverteilungen der HCT-Rohwerte für zwei Altersgruppen (Daten aus Heaton et al., 2004)
Linearisierung der Messskala
Beim HCT gab es die seltene Gelegenheit, dass für die Linearisierung auf empirische Daten zurückgegriffen werden konnte, wenn auch nur in zusammengefasster Form und mit gewissen Kompromissen. In der oben schon erwähnten großen Studie von Heaton et al. (2004)13) war eine Flächentransformation der Fehlerrohwerte in normalverteilte Standardwerte durchgeführt worden. Leider war dies nur über die Gesamtstichprobe erfolgt, was nicht ideal ist, weil sich in dieser heterogenen Stichprobe neben den hier interessierenden Einflüssen der Skala noch weitere Effekte spiegeln, die die Verteilungsform beeinflussen. Insbesondere sind dies Effekte des Alters, gerade bei einem so altersensitiven Test wie dem HCT. Aber immerhin, aus den Daten ließ sich nach Verstetigung und Glättung der Wertpunktskala eine fein gradierte Wertetabelle erstellen, die als Grundlage für die Linearisierung der Leistungswerte dienen konnte.
Für die Berechnung der Leistungswerte braucht man allerdings die Daten einer jungen gesunden Stichprobe. Die sind im Handbuch von Heaton et al. (2004) nicht separat dargestellt. Die Autoren hatten den Weg gewählt, mittels einer polynomialen Regression die Einflüsse von Alter, Geschlecht und Ausbildungsjahren auf die Rohwerte zu berechnen. Die Ergebnisse sind in Form von alters-, geschlechts- und ausbildungskorrigierten T-Werten tabelliert. Die Ausbildungsdauer der Gesamtstichprobe von Heaton et al. (2004) wich deutlich vom amerikanischen Durchschnitt nach oben ab. Für die Berechnung der Leistungswerte wurde deshalb nur auf die Teilstichprobe mit 12-jähriger Ausbildungsdauer zurückgegriffen (N=114). Dies entsprach damals dem Mittelwert der Ausbildungsdauer der amerikanischen Bevölkerung. Wegen der relativ groben Einteilung wäre eine breitere Bereichsbildung nicht möglich gewesen. Dabei hätte man eine große Abweichung vom Durchschnitt in Kauf nehmen müssen, was als schwererwiegend eingeschätzt wurde. Wie weiter unten dargestellt, entsprach die Leistung der hier gewählten Teilstichprobe relativ gut der Leistung der metaanalytisch verrechneten Stichproben.
Normempfehlungen in der Literatur
Halsteads Category Test wird seit rund 60 Jahren angewendet. Wie viele klassische neuropsychologische Tests wurde er damals ohne ausreichende Normdatenbasis publiziert. In der Originalpublikation wurde lediglich ein oberer Grenzwert für den Normalbereich der Fehlerzahl angegeben. Für die anfangs benutzte Form mit 336 Items (Halstead, 1947)14) wurde ein Grenzwert von 80 genannt, was später rein rechnerisch auf die seit ca. 1950 eingesetzte Version mit 208 Items 15) übertragen wurde und in eine Grenzwertempfehlung von 50 mündete. Angesichts der hohen Korrelationen des CT mit Intelligenz, Bildung und Alter war das schon immer viel zu grob, selbst wenn man berücksichtigt, dass die weitere Interpretation der Testergebnisse auf dem Hintergrund klinischer Erfahrungen und meistens auch im Zusammenhang mit weiteren testpsychologischen Untersuchungen erfolgte.
Im Laufe der Zeit wurden für den HCT in vielen Buch- und Zeitschriftenbeiträgen neben Daten von klinischen Gruppen auch solche von gesunden Probanden publiziert – ein Vorteil, den der HCT ebenfalls mit klassischen neuropsychologischen Verfahren teilt (etwa mit dem Trail Making Test, der Rey-Figur, Wortlisten-Gedächtnistests und Wortflüssigkeitstests). Beim HCT kann man inzwischen auf eine stattliche Zahl untersuchter Probanden aller Altersgruppen zurückgreifen.
Häufig benutzen klinische Psychologen in ihrer praktischen Tätigkeit eine einzige dieser Normquellen. Die Auswahl dürfte meist eher pragmatischen (Bekanntheit, Verfügbarkeit) als systematischen Gesichtspunkten folgen. Die systematischen Übersichten in den neuropsychologischen Standardwerken helfen auch nicht immer bei der Auswahl. So werden zum Beispiel in der vierten Auflage des Standardwerks „Neuropsychological Assessment“ (Lezak, Howieson, & Loring, 2004)16) drei durchaus unterschiedliche Normdatensätze mit Literaturangaben zitiert, ohne dass eine Präferenz der AutorInnen für einen davon erkennbar wäre. In Spreen & Strauss' (1998) „A Compendium of Neuropsychological Tests“ 17) ist die Darstellung der Normensituation noch verwirrender. Einerseits wird die an Gesunden durchgeführte Normierung von Heaton et al. (1991) 18) zwar erwähnt, allerdings wird die Stichprobengröße (N=486) als „very small“ abqualifiziert. Auf der anderen Seite werden die an 112 Patienten diverser Kliniken erhobenen Daten von Alekoumbides et al. (1987) 19) gebrauchsfertig auf drei Buchseiten wiedergegeben, ohne dass der Stichprobenumfang und die Herkunft der Daten auch nur erwähnt wären.
Normerstellung
Für die Erstellung der TDB2-Normen des HCT wurde eine weniger eklektische Strategie gewählt. Zunächst wurden systematisch Studien gesucht, in denen HCT-Daten gesunder Probanden enthalten waren. Da es sich bei dem HCT um einen weitgehend sprachfreien Test handelt, wurde dabei auf eine Beschränkung der nationalen und/oder sprachlichen Herkunft der Normdaten verzichtet. Die Bedingung für den Einschluss einer Studie war, dass Mittelwerte und Standardabweichungen der Fehlerrohwerte einer Stichprobe von gesunden Probanden in einem oder mehreren differenzierten Altersbereichen berichtet wurden. Es ließen sich 10 Studien lokalisieren, in denen Normdaten von 1622 Probanden im Altersbereich zwischen 15 und 84 Jahren angegeben waren. Mit Hilfe einer metaanalytischen Zusammenfassung wurden diese Normen integriert und damit von den Eigenheiten der einzelnen Studie unabhängiger gemacht.
Normquellen
Für die hier errechneten Normen des HCT gab es zwei große Referenzwerke. Das eine ist eine Sammlung von Normdaten für eine Reihe von neuropsychologischen Standardverfahren, die unter dem Titel Handbook of Normative Data for Neuropsychological Assessment als Monographie publiziert wurde (Mitrushina et al., 1999)20). Für den HCT werden in diesem Handbuch insgesamt 19 Studien mit Normdaten besprochen. Sechs davon, nämlich die als Studien 521), 622), 923), 1224), 1325) und 1826) genannten, erfüllten unsere Einschlusskriterien. Von Studie 5 wurden nur die beiden Gruppen im IQ-Bereich zwischen 89 und 112 einbezogen. Ausschlussgründe für die anderen Studien waren: ein zu weiter, undifferenzierter Altersbereich in den Studien 1, 2, 3, 7, 11, 14, 16, 17 und 19 (Literaturangaben dazu bei Mitrushina et al., 1999) sowie der Einbezug kranker Personen in die Stichproben der Studien 4 und 8.
Eine Besonderheit stellen die Studien 1027) und 1528) dar. Beide wurden nicht einbezogen, weil sie Vorläuferstudien zu einem neueren Normierungshandbuch29) sind, das die älteren Daten einbezieht. In der revidierten Version dieses Normenhandbuchs30) sind ausführliche, statistisch aufgearbeitete Daten einer Stichprobe von 1212 gesunden US-Bürgern enthalten, die fast alle zur Halstead-Reitan Neuropsychologischen Testbatterie gehörenden Verfahren und weitere Intelligenztests durchgeführt haben. Dieses Handbuch spielt für die psychometrische Aufarbeitung der HCT-Daten eine besondere Rolle. Die Linearisierung der Skala beruht ausschließlich auf den Daten dieser Studie. In die Metaanalyse konnte allerdings nur eine Teilstichprobe dieser Studie, nämlich die weißen US-Amerikaner mit einer 12-jährigen Ausbildungsdauer, einbezogen werden, weil die Stichprobe ein sehr hohes Bildungsniveau hatte. Selbst diese Teilstichprobe liefert aber mit 320 Personen im Altersbereich zwischen 20 und 84 noch den zweitgrößten Beitrag zur HCT-Normierung. Wichtig ist dabei auch der Gesichtspunkt, dass das Handbuch auch die Ergebnisse weiterer Tests enthält, unter anderem die Trail Making Tests, bei denen sie auch einen wesentlichen Beitrag zur Normierung leisten. Da die Stichprobe von Heaton et al. (2004) die einzige ist, deren Werte als Perzentilverteilung vorlagen und nicht nur als Mittelwert und Standardabweichung, die über Simulationsrechnungen nachträglich normalisiert werden mussten, geht sie mit dem gleichen Beitrag in die Gesamtnormierung ein wie die restlichen Studien zusammen.
Drei weitere Stichproben, die nicht bei Mitrushina et al. (1999) gelistet sind, wurden ebenfalls in die Metaanalyse mit einbezogen:
- In einer kleineren Normuntersuchung31) wurden 101 gesunde Probanden im Alter zwischen 18 und 85 Jahren mit dem HCT und anderen neuropsychologischen Verfahren untersucht. Trotz der relativ geringen Stichprobengröße zeichnete sich diese Untersuchung dadurch aus, dass Alter, Ausbildung und Geschlecht der Probanden weitgehend dem Bevölkerungszensus entsprachen.
- Elias et al.32) berichteten 1993 über Alters- und Geschlechtseffekte bei neuropsychologischen Testleistungen an Hand einer Stichprobe von 427 gesunden Probanden im Altersbereich zwischen 15 und 74. Kritisch ist bei dieser Studie anzumerken, dass das Ausbildungsniveau im Bereich zwischen 12 und 19 Jahren lag und damit sicher höher war als bei den meisten anderen Untersuchungen.
- Eine kleinere Studie33) berichtete für den engen Altersbereich zwischen 17 und 34 Jahren über HCT-Ergebnisse von 51 gesunden College-Studenten, auch dies also eine Studie mit relativ hohem Ausbildungsniveau.
Eine weitere Normquelle für den HCT wäre eigentlich auch das Halstead-Russell Neuropsychological Evaluation System (HRNES-R;Russell & Starkey, 2001).34) Russell und Koautoren haben über viele Jahre hinweg eine Gruppe von rund 200 Personen, meist Männer, mittleres Alter 48 Jahre, zusammengestellt, die wegen Verdacht auf neurologische Störungen untersucht wurden, bei denen aber auch bei sorgfältiger Untersuchung keine Defizite nachgewiesen werden konnten. Im HRNES-R wird diese Gruppe als Kontrollgruppe bezeichnet. Im Manual sind die Original-Rohwerte des HCT für diese Gruppe leider nicht enthalten. Stattdessen lassen sich „Erwartungswerte“ für sieben Altersgruppen und vier Bildungs- oder IQ-Gruppen nachschlagen, die allerdings durch lineare Regressionen berechnet wurden. Im mittleren Alters- und IQ-Bereich entsprechen die Werte dem Mittelwert der anderen in die Metaanalyse einbezogenen Studien. Im hohen Altersbereich sind die Mittelwerte aber deutlich niedriger, was wohl mehr auf die Regressionsanalyse zurückgeht, die (fälschlicherweise) Homoskedastizität annimmt. Durch den Einbezug dieser Normen hätte man zumindest in Teilbereichen mehr Artefakte importiert, weshalb darauf verzichtet wurde. Speziell Lezak et al. (2004)35) bestreiten auch den Status der Probanden von Russell & Starkey (2001)36) als „normale Probanden“, was aber von Russell verschiedentlich 37)38) zurückgewiesen wurde.
Tabelle 1: Übersicht über die metaanalytisch verrechneten Normierungsstudien
| Erstautor | Jahr | Altersbereich | N | Ausbildung | IQ | % m. | Land |
|---|---|---|---|---|---|---|---|
| Wiens | 1977 | 21-28 | 48 | 14 | 117 | 100 | USA |
| Mack | 1978 | 20-37 und 60-80 | 81 | 14 | 116+-4 | 15 | USA |
| Pauker | 1980 | 19-71 | 147 von 363 | 89-112 | 42 | Kanada | |
| Fromm-Auch | 1983 | 15-64 | 190 | 14,8+-3 | 119+-9 | 58 | Kanada |
| Yeudall | 1987 | 15-40 | 225 | 14,9+-3 | 114+-10 | 56 | Kanada |
| El-Sheikh | 1987 | 17-24 | 32 | 14 | 100 | Ägypten | |
| Krey | 1993 | 18-85 | 101 | 13 | 105 | 38 | D |
| Elias | 1993 | 15-74 | 427 | 14,5+-2 | 44 | USA | |
| Titus | 2002 | 17-34 | 51 | 107 | 37 | USA | |
| Heaton | 2004 | 20-84 | 320 von 1212 | 12 | 66 | USA |
Insgesamt wurden in die metaanalytische Normierung des HCT 1622 Personen einbezogen. Tabelle 1 gibt einige Details der Studien. Man sieht, dass auch die Gesamtstichprobe noch immer eine relativ hohe Schulausbildung aufweist. Von den ersten 9 Studien lagen nur Mittelwerte und Standardabweichungen pro Altersgruppe vor. Bei Heaton et al. (2004) waren die mitgeteilten Daten umfangreicher, weswegen sie mit höherem Gewicht in die Metaanalyse eingingen.
Metaanalytische Zusammenfassung der Normdaten
siehe ausführliche Dokumentation
Leistungs- und Altersnormen im Überblick
siehe ausführliche Dokumentation
Diskussion
In der zweiten Auflage des neuropsychologischen Datenhandbuchs von Matrushina et al. (2005) finden sich für viele neuropsychologische Testverfahren Metaanalysen vorhandener Normquellen in der Literatur. Die Vorgehensweise der Autoren unterscheidet sich von der in TDB2Online vor allem in zwei Punkten:
- Die Metaanalysen von Mitrushina et al. sind regressionsbasiert: Mittelwerte und Standardabweichungen von Teilstichproben, die sich nach Alter, Geschlecht und Ausbildungsjahren charakterisieren lassen, werden mit Regressionsanalysen integriert. Finden sich Effekte der demographischen Variablen, werden Mittelwerte und Standardabweichungen für Teilgruppen geschätzt. Für das Alter finden sich fast immer Effekte, hier erfolgt die Angabe in Fünf-Jahres-Altersintervallen, wenn die Daten es hergeben. Für andere demographische Variablen werden seltener Effekte gefunden.
- Alle Analysen finden auf Rohwertebene statt, die Verteilungen der Rohwerte werden nicht weiter berücksichtigt.
Für den HCT wurden 22 Studien beschrieben und 21 davon tabellarisch zusammengefasst. 11 Studien wurden in die Metaanalyse aufgenommen (mir ist nicht klar geworden, welche das waren). Das Alter der Probanden hatte einen starken Effekt auf Mittelwerte und Standardabweichungen. Für Fünf-Jahres-Gruppen wurden Mittelwerte und Standardabweichungen regressionsanalytisch geschätzt und die Ergebnisse als Gleichung und als Tabelle ausgegeben. Da die Tabelle einen Druckfehler enthält (eine Altersgruppe fehlt, deshalb verschieben sich die Ergebnisse), wurden die erwarteten Werte für die Darstellung hier im Wiki mit Hilfe der Gleichungen geschätzt.
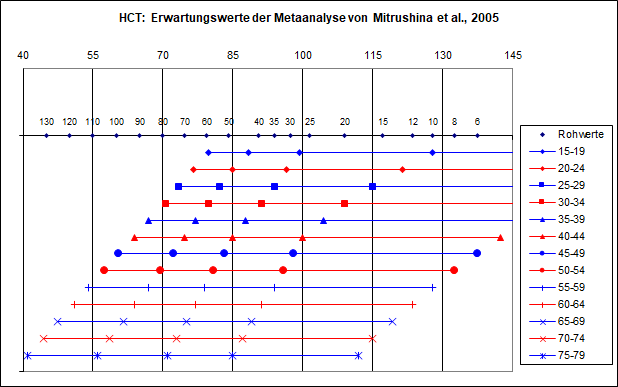
Abbildung 6 zeigt die Ergebnisse der Metaanalyse von Mitrushina et al. (2005) in einer Form, die einen Vergleich mit den TDB2Online-Normen ermöglicht. Für jede Altersgruppe wurden aus den vorhergesagten Mittelwerten und Standardabweichungen die Rohwerte an den Stellen Mittelwert minus zwei Sigma, Mittelwert minus ein Sigma, Mittelwert, Mittelwert plus ein Sigma und Mittelwert plus zwei Sigma berechnet und in das TDB2Online Leistungswertgitter eingezeichnet.
Abbildung 6: Ergebnisse der Metaanalyse von Mitrushina et al. (2005) als Mittelwerte plus/minus ein und zwei Sigma, aufgetragen im Leistungswertgitter von TDB2Online.
Schaut man sich nur die Mittelwerte an, dann gibt es keinen gravierenden Unterschied zwischen den Normen von Mitrushina und denen von TDB2Online. Im gesamten Altersverlauf bewegen sich die Mittelwerte vom Leistungswert 100 bei den Jungen bis zu etwa 70 bei den Alten, in beiden Datenaufbereitungen. Dies entspricht Rohwerten von etwa 27 bis 80. Auch wenn sich in den mittleren Altersgruppen Unterschiede von bis zu 10 Rohwerten finden, sind die Mittelwerte über alles doch stabil genug, dass sie mit der Regressionsstatistik zurechtkommen.
Problematisch wird es dagegen, wenn man die Standardabweichungen betrachtet, die man für die Skalierung der altersbezogenen Standardwerte braucht. Hier kommt der rohwertbezogene analytische Ansatz der Regressionsanalyse schnell an seine Grenze. In allen Altersgruppen sind die Werte für sehr gute Leistungen (Mittelwert plus zwei Sigma) zu hoch, in den jüngeren Altersgruppen unter 30 Jahren viel zu hoch: Der Versuch, sie zu berechnen, führt zu negativen Rohwerten. Ein Mittelwert von 27 und eine Standardabweichung von 16 gehen nicht gut zusammen, wenn bei einem Rohwert von circa 8 der mögliche Rohwertbereich endet. Bei der gegebenen Schiefe der HCT-Rohwertverteilung ist die formale Anwendung von parametrischen Statistiken auf Rohwertebene nicht sinnvoll. Die Effekte spielen sich vor allem in den Außenbereichen der Verteilungen ab, weniger um den Mittelwert herum.